Question

What is the correct answer to this question A. 38B. 46C:29D:58

Answer 1

Given that

The rectangle is there with length, WX = 4x + 10 and breadth, XY = 2x - 6

Also, the perimeter is 116 and we have to find the value of WX.

Explanation -

The formula for the perimeter of the rectangle is given as P

`\begin{gathered} Perimeter=2*(l+b) \\ where\text{ l = length and b = breadth} \end{gathered}`

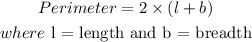
On substituting the values we have

`\begin{gathered} 116=2*(4x+10+2x-6) \\ (116)/(2)=6x+4 \\ 58=6x+4 \\ 6x=58-4 \\ 6x=54 \\ x=(54)/(6) \\ x=9 \end{gathered}`

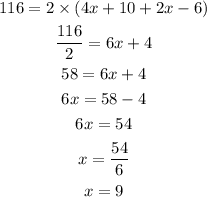
So now WX,

WX = 4x + 10

WX = 4(9) + 10

WX = 36 + 10 = 46

WX = 46

H

So the final answer is 46.