Question

calculate the average rate of change between consecutive data points in parts A through C to determine whether the output in each table is a linear function of the input A) input -5 0 5 8 output -50 -5 40 67B) input 2 7 9 14 output 0 15 18 20C) input -4 0 3 5 output 25.8 1 21.1 34.5A) Select the correct choice below and if necessary, fill-in the answer box to complete your choice. a) The average rate of change between consecutive data points in table a is ___ Thus, the output is a linear function of the input(simplify answer) b) The output is not a linear function of the input.

Answer 1

Given:

The table:

The rate of change is gotten by using the slope formula;

To get the rate of change between inputs -5 and 0

`\begin{gathered} The\text{ points are:} \\ (-5,-50)\text{ and }(0,-5) \\ where: \\ x_1=-5,y_1=-50 \\ x_2=0,y_2=-5 \\ \\ Hence, \\ m=(-5-(-50))/(0-(-5)) \\ m=(-5+50)/(0+5) \\ m=(45)/(5) \\ m=9 \end{gathered}`

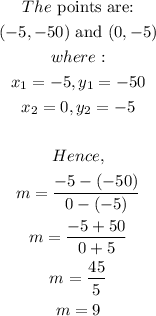
To get the rate of change between inputs 0 and 5

`\begin{gathered} The\text{ points are:} \\ (0,-5)\text{ and }(5,40) \\ where: \\ x_1=0,y_1=-5 \\ x_2=5,y_2=40 \\ \\ Hence, \\ m=(40-(-5))/(5-0) \\ m=(40+5)/(5-0) \\ m=(45)/(5) \\ m=9 \end{gathered}`

To get the rate of change between inputs 5 and 8

`\begin{gathered} The\text{ points are:} \\ (5,40)\text{ and }(8,67) \\ where: \\ x_1=5,y_1=40 \\ x_2=8,y_2=67 \\ \\ Hence, \\ m=(67-40)/(8-5) \\ m=(27)/(3) \\ m=9 \end{gathered}`

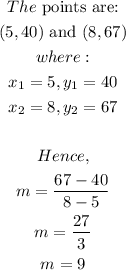
From the calculations, it can be seen that the rate of change for each consecutive point is 9.

Therefore, the average rate of change between consecutive data points in table A is 9.

Thus, the output is a linear function of the input.