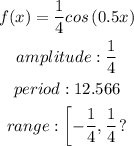Given:
There are given the trigonometric function:
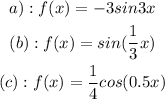
Step-by-step explanation:
From the equation (a):
The amplitude is defined when displacement or distance is moved by a point from the equilibrium position.
So,
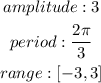
From the function (b):
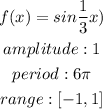
And,
From the function (c):