Question

The square in the figure has two sides tangent to the circle. If area of the circle is 9a^2pi^2, find the area of the square. (A=6, pi=3.14, please estimate the answer two places after decimal)

Answer 1

As the square has two sides tangent to the circle, the lenght of the side will be de diameter of the circle.

The area of a circle, which is pi*r², in this case is 9a²pi², given that a=6.

So:

`\begin{gathered} \pi r^2=9\cdot a^2\cdot\pi^2\text{ (dividing both sides by pi)} \\ \pi r^2=9\cdot36\cdot3.14^(2) \\ \pi r^(2)=3,194,51 \\ r^(2)=1017,36 \\ r=31,89 \end{gathered}`

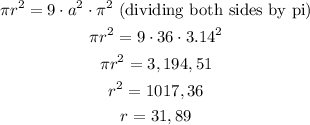
Once r=31.89,, the diameter will be 2*r= 63.78

The area of the square is (63.78)² = 4,067.89u²