Question

5Trent's watch runs at half the speed itshould. In other words, the hands on thewatch move only a half hour when an hourof time has really passed. If Trent sets hiswatch correctly at 8 am, what time will itshow when the real time is 10:30 a,m.?fan

Answer 1

We are told to find what time Trent's watch will show when the real-time is 10:30 am

To do so, we will find the rate at which his watch moves

The rate is calculated as follow

`Rate=\frac{\text{time covered}}{time\text{ elapsed}}`

`\begin{gathered} \text{Rate}=\frac{(1)/(2)\text{hour}}{1\text{hour}}=(1)/(2)=0.5 \\ \\ \text{Rate}=0.5 \end{gathered}`

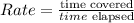
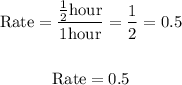
With this rate, we can get the actual time the watch will show when the real-time is 10:30 am by multiplying the rate by the time difference

`10\colon30am-8am=2\colon30\text{ hours}`

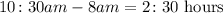
This time will then be converted to minutes

`2\colon30\text{hours = 2(60)+30=120+30=150 minutes}`

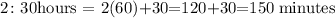
We will multiply this time in minutes by the rate

`\begin{gathered} =0.5*150 \\ =75\text{ minutes} \end{gathered}`

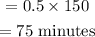
So the time will be

`\begin{gathered} 8\colon00+0\colon75 \\ =8\colon00+1\colon15 \\ =9\colon15am \end{gathered}`

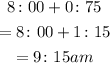
Thus, the time will be 9:15 am