Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. Austin plans to attend the Perry County Fair and is trying to decide what would be a better deal. He can pay $40 for unlimited rides, or he can pay $16 for admission plus $2 per ride. If Austin goes on a certain number of rides, the two options wind up costing him the same amount. What is that cost? How many rides is that?

Answer 1

Austin has two options:

Option 1: Pay $40 for unlimited rides

Option 2: pay $16 plus $2 per ride

For the two options to end up costing the same amount, the second option needs to end up being $40, because the payment in the first option is already fixed to $40.

That answers the first question:

What is the cost? $40

Now we need to find how many rides are needed for the second option to cost $40.

We will call the number of rides "x", and thus, since in the 2nd option there is an admission cost of 16 and a cost of $2 per ride, the expression that represents the cost is in option 2 is:

`16+2x`

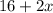
And since we know that the cost has to be $40 to be equal to the cost of option 1:

`16+2x=40`

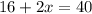
And now we solve this equation for the number of rides x.

First, Subtract 16 to both sides of the equation:

`16-16+2x=40-16`

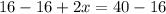
On the left side, 16-16 cancel each other, and on the right side 40-16 is 24, thus:

`2x=24`

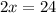
Finally, divide both sides of the equation by 2 to find the value of x:

`\begin{gathered} (2x)/(2)=(24)/(2) \\ \\ x=12 \end{gathered}`

The number of rides for the second option to be equal in cost to the first option is 12 rides.

Answer:

The cost is $40 and the number of rides is 12.