Question

Given cos A = and that angle A is in Quadrant II, find the exact value ofAcsc A in simplest radical form using a rational denominator.89

Answer 1

cscA is the inverse of the sine of A.

`cscA=(\sin A)^(-1)`

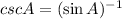
Since we know the value for the cosine, using the identity

`\sin ^2A+\cos ^2A=1`

We can calculate the value for the sine.

`\begin{gathered} (-\frac{8}{\sqrt[\square]{89}})^2+\sin ^2A=1 \\ (64)/(89)+\sin ^2A=1 \\ \sin ^2A=1-(64)/(89) \\ \sin A=\pm\sqrt[]{(25)/(89)} \\ \sin A=\pm\frac{5}{\sqrt[]{89}} \end{gathered}`

Since we know that the angle A is located at the Quadrant II, we know its sine is positive, then

`\sin A=\frac{5}{\sqrt[]{89}}`

Now, using our first relation

`\csc A=(\frac{5}{\sqrt[]{89}})^(-1)=\frac{\sqrt[]{89}}{5}`

And this is our final answer.