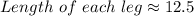Question

If a 45° - 45° - 90° triangle has a hypotenuse of 7.07. Find the length of each leg, rounding to the nearest tenth.

Answer 1

12.5

Explanation:

The internal equation is very indefinite

Answer 2

Given a 45°- 45°-90° triangle, you know that the length of its hypotenuse is:

`c=7.07`

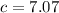
By definition, the hypotenuse of a 45°- 45°- 90° triangle is given by:

`c=2√(a)`

Where "c" is the length of the hypotenuse and "a" is the length of one leg, because the legs of a 45°- 45°- 90° triangle have the same length.

Therefore, you can substitute the length of the given hypotenuse into the formula and solve for "a", in order to find the length of each leg of the triangle:

`7.07=2√(a)`
`(7.07)/(2)=√(a)`
`((7.07)/(2))^2=a`
`a\approx12.5`

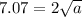
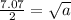
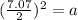
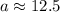
Hence, the answer is:

`Length\text{ }of\text{ }each\text{ }leg\approx12.5`