Question

In the above triangle, would you use SINE, COSINE, or TANGENT to solve for the missing side (TYPE IN ALL CAPS) The measure of the missing angle is (ROUND TO THE NEAREST DEGREE). 1 2 3 4 5 6 7 8 9

Answer 1

Once we know the measure of the unknown angle, we can relate its value with the opposite side which measure 10 units and the hypotenuse of 39 units by means of the cosine and tangent functions, that is,

`\begin{gathered} \cos \text{ ? =}\frac{\text{ adjacent side to ?}}{\text{hypotenuse}}=(x)/(39) \\ \tan \text{ ? =}\frac{\text{ opposite side to ?}}{\text{adjacent side to ?}}=(10)/(x) \end{gathered}`

where x denotes the missing side.

Would you use SINE, COSINE or TANGENT to solve for the missing side? Answer: COSINE and TANGENT.

Now, in order to find the missing angle, we must use the sine function because it relates the leg 10 with the hypotenuse of 39 units, that is,

`\sin \text{ ? =}\frac{\text{ opposite side to ?}}{\text{hypotenuse}}=(10)/(39)`

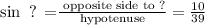
which gives

`\text{ sin ? =}0.2564`

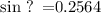
So, by applying the inverse sine function to both sides, we have

`\begin{gathered} \text{ ? =sin}^(-1)(0.2564) \\ \text{ ? = 14.857 degre}es \end{gathered}`

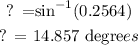
Therefore, by rounding to the nearest degree, the measure of the missing angle is 15 degrees