Question

Which expression is equivalent to X^2 + 2x + 2? Answer: (x - 1 + i) (x - 1 - i) (x + 2) (x + 1 ) (x + 1 - i ) (x + 1 + i) (x + 1 - i) (x + 1 -i)

Answer 1

Consider the given expression,

`x^2+2x+2`

Consider the properties,

`\begin{gathered} i^2=-1 \\ i^3=-i \\ i^4=1 \end{gathered}`

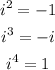
Let us check each expression, and the one which upon simplification gives the identical quadratic expression will be the correct choice.

Solve the first option,

`\begin{gathered} (x-1+i)(x-1-i) \\ =(x-1)^2-(i)^2 \\ =(x^2-2x+1)-(-1) \\ =x^2-2x+1+1 \\ =x^2-2x+2 \end{gathered}`

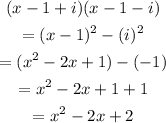
Since this is not identical to the given quadratic polynomial, first option is incorrect.

Solve the second option,

`\begin{gathered} (x+2(x+1) \\ =x(x+1)+2(x+1) \\ =x^2+x+2x+2 \\ =x^2+3x+2 \end{gathered}`

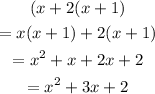
Since this is not identical to the given quadratic polynomial, second option is incorrect.

Solve the third option,

`\begin{gathered} (x+1-i)(x+1+i) \\ =(x+1)^2-(i)^2 \\ =(x^2+2x+1)-(-1) \\ =x^2+2x+1+1 \\ =x^2+2x+2 \end{gathered}`

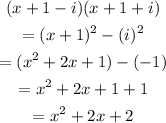
Since this is identical to the given quadratic polynomial, third option is incorrect.

Thus, the third expression is equivalent to the given quadratic polynomial.