Answer:
There are 13,917.2 moles of argon.
Step-by-step explanation:
1st) The given information from the exercise is:
- Volume (V): 2500L
- Pressure (P): 13790kPa
- Temperature (T): 25°C
It is important to conver all the variables units to liters, atm and Kelvin:
- Conversion from kPa to atm:
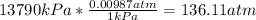
- Conversion from °C to K:
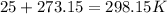
2nd) Now we can replace the values of pressure, volume and temperature in the Ideal Gases formula to calculate the number of moles:
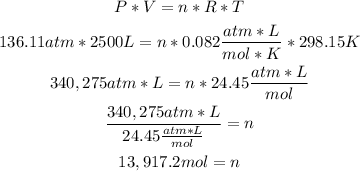
Finally, there are 13,917.2 moles of argon.