In general a trigonometric function of the form:
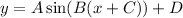
has the following properties:
• A is the amplitude.
,
• C is the phase shift (positive to the left)
,
• D is the vertical shift
,
• The period is given as:
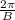
From the information given we have that the amplitude is 3, then:
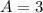
The period is 6pi then we have:
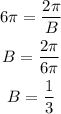
The horizontal shift is:
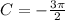
And the vertical shift is:
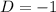
Once we know the values we plug them in the general expression for the sine function, our function is:
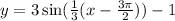
Now that we have the function we can find the its value when x=2pi, plugging this value of x in the expression we have:
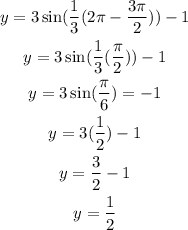
Therefore, the value of y for the given x is 1/2