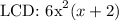Question

What is the least common denominator of the rational expressions below ?5/x^2-3/5x^2+12x

Answer 1

`\text{LCD: 6x}^2(x+2)`

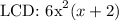
Explanation:

*LCD is the lowest common multiple of the denominators of a set of fractions.

As a first step, factor each denominator as much it can be factored:

`\begin{gathered} x^2=x\cdot x \\ 6x^2+12x=6x(x+2) \end{gathered}`

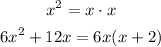
Then, determine the maximum number of times they occur in any factorization to find the LCD:

`\text{LCD: 6x}^2(x+2)`