Question

Find the missing measurements in the shape below. Then break apart the shape into two rectangles to find its area.

Answer 1

`30m^2`

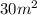
Step-by-step explanation

The length of the base of the shape is 8 m.

Since the top of the shape is of equal length to the base length, it implies that the sum of ? and 5 m must be equal to 8 m. That is:

`\begin{gathered} \text{?}+5=8 \\ \Rightarrow?=8-5 \\ ?=3m \end{gathered}`

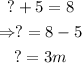
The same principle applies to the length of the left side of the shape. This implies that the sum of ? and 3 m is equal to 5 m. That is:

`\begin{gathered} ?+3=5 \\ \Rightarrow?=5-3 \\ ?=2m \end{gathered}`

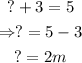
Now, we can divide the shape into two rectangles to find the area:

The area of the shape is equal to the sum of the areas of rectangles A and B.

The area of a rectangle is:

`A=L\cdot W`

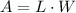
where L = length, W = width

Therefore, the area of A is:

`\begin{gathered} A=3\cdot2 \\ A=6m^2 \end{gathered}`

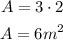
and the area of B is:

`\begin{gathered} A=8\cdot3 \\ A=24m^2 \end{gathered}`

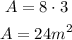
Hence, the area of the shape is:

`\begin{gathered} A=6+24 \\ A=30m^2 \end{gathered}`

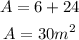
The area is 30 square meters.