Question

A random sample of 120 middle school kids in LA showed that 88 have a smartphone.Construct a 95% confidence interval for the proportion of students who have a smartphone. Is it reasonable to claim that 90% have one? Why?

Answer 1

To solve this we will apply the formula

`C.I=p\pm Z(\alpha)/(2)\sqrt{(p(1-p))/(n)}`

The required probability p becomes

`\begin{gathered} p=(88)/(120)=0.73 \\ n=sample\text{ size}=120 \\ Z(\alpha)/(2)=Z_(0.95)=1.96 \end{gathered}`

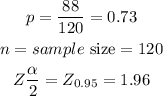
Note that the Z score was gotten using a calculator.

Plugging in the values we have

`\begin{gathered} C.I=p\pm Z(\alpha)/(2)\sqrt{(p(1-p))/(n)} \\ C.I=0.73\pm1.96\sqrt{(0.73(1-0.73))/(120)} \\ C.I=0.73\pm1.96\sqrt{(0.73(0.27))/(120)} \\ C.I=0.73\pm1.96*0.0405277 \\ C.I=0.73\pm0.07943 \end{gathered}`

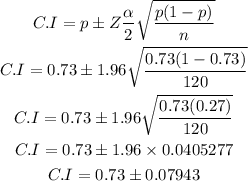
So, we have

`\begin{gathered} 0.73+0.07943 \\ =0.8094344\text{ = 80.94\%} \\ and\text{ } \\ 0.73-0.07943 \\ =0.65057=65.06\% \end{gathered}`

So we have the interval as (65.06%, 80.94%).

Since the confidence interval does not fall around 90%, but less than 90%

Hence it is not reasonable to claim that 90% have one

You wel