Question

Determine whether the function is continuous on the entire real number line. Explain your reasoning.

Answer 1

So,

Given the function:

`f(x)=(4)/(x^2-36)`

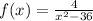
To check if the function is continuous in the entire number real line, we need to analyze the restrictions in the domain.

As you can notice, the denominator of a rational function can't be zero, so:

`x^2-36\\e0`

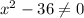
We're going to find the values of x such that:

`x^2-36=0`

This is:

`\begin{gathered} x^2=36 \\ x=\pm6 \end{gathered}`

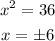
As you can see, "x" can't take the values of 6 and -6. If that happens, the function is not defined. Thus, the function is not continuous on the entire real number line.