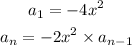1) Given this Explicit formula, let's find a_1, and then a_2 and then compare both terms:
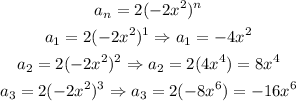
2) Comparing both terms we can state that this is a Geometric Sequence we can write its ratio as:

3) So we can write our Recursive formula as:
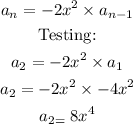
So the answers are: