Question

Suppose that the mean systolic blood pressure for women over age seventy is 131 mmHg (millimeters of mercury), with a standard deviatiob of 9 mmHg. Supposed that the blood pressures are normally distributed. Complete the following statements. Choose the correct answer (68,75,95,99.7)

Answer 1

(a)Approximately 99.7% of women over 70 have blood pressures between 104 mmHg and 158 mmHg.

(b)Approximately 68% of women over 70 have blood pressures between 122 mmHg and 140 mmHg.

Explanation:

Given:

• Mean = 131 mmHg

,

• Standard Deviation = 9 mmHg.

By the empirical rule, in a normal distribution:

• 68% of the data falls within one standard deviation.

,

• 95% percent within two standard deviations, and

,

• 99.7% within three standard deviations from the mean.

(a)

As given by the empirical rule above, 99.7% of data in a normal distribution falls within three standard deviations from the mean. That is:

`\mu\pm3\sigma`

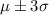
Substitute the given values:

`\begin{gathered} 131\pm3(9)=131\pm27 \\ =(131-27,131+27) \\ =(104,158) \end{gathered}`

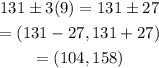
Approximately 99.7% of women over 70 have blood pressures between 104 mmHg and 158 mmHg.

(b)As given by the empirical rule above, 68% of data in a normal distribution falls within one standard deviation from the mean. That is:

`\mu\pm\sigma=(131-9,131+9)=(122,140)`

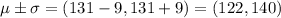
Approximately 68% of women over 70 have blood pressures between 122 mmHg and 140 mmHg.