Question: Liliana has $3.80 in nickels and quarters in her purse. She has 22 more nickels than quarters. How many coins of each type does she have?
Solution:
Liliana has $3.80 in nickels and quarters in her purse.
She has 22 more nickels than quarters.
We first have to establish a system of equations. Since we have two unknown variables, we need to have two equations. The first equations;
let x = number of quarters
x+22 = number of nickels
The total worth of coins = $3.80
The value of a quarter is $0.25 and the value of a nickel is $0.05.
According to the problem:
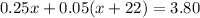
Applying the distributive property, we get:
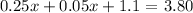
this is equivalent to:
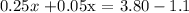
this is equivalent to:
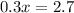
Solving for x, we obtain:
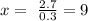
Thus, we obtain that:
The number of quarters = x = 9
number of nickels = x+22 = 9+22 = 31
So t