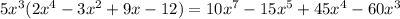To simplify the polynomial, use the distributive property to expand the parenthesis:
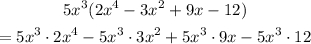
Next, use the properties of exponents to simplify the products between the powers of the variable x. Multiply the numerical factors to find the coefficient of each term:
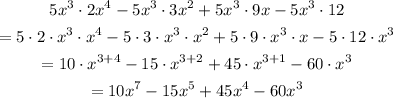
Therefore, the simplified form of the given polynomial, is: