SOLUTION
Given the question, the following are the solution steps to answer the question.
STEP 1: Represent the two daughters with a variable
Let the first daughter represented with y
Let the second daughter be represented with z
STEP 2: Interpret the statements in the question

STEP 2: Write out the two gotten equations
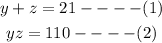
STEP 3: Make y the subject of the equation 1
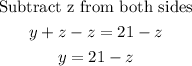
STEP 4: Substitute the value for y in equation 2
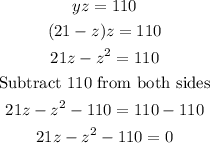
STEP 5: We solve the quadratic equation to get the values of z
![\begin{gathered} 21z-z^2-110=0 \\ \mathrm{Write\: in\: the\: standard\: form}\: ax^2+bx+c=0 \\ z^2+21z-110=0 \\ \text{ Using quadratic formula;} \\ z_(1,\: 2)=(-21\pm√(21^2-4\left(-1\right)\left(-110\right)))/(2\left(-1\right)) \\ 21^2-4(-1)(-110)=\sqrt[]{1}=1 \\ z_(1,\: 2)=(-21\pm\:1)/(2\left(-1\right)) \\ \mathrm{Separate\: the\: solutions} \\ z_1=(-21+1)/(2\left(-1\right)),\: z_2=(-21-1)/(2\left(-1\right)) \\ z_1=(-20)/(-2)=10 \\ z_2=(-22)/(-2)=11 \\ z=10,\: z=11 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fn2q4zm4r3klef0bzwubmzk3qv4iame1pp.png)
STEP 6: Get the age of the other daughter
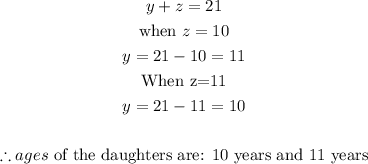
Hence, the age of Mr. Thaxton's youngest daughter is 10 years