Given the equation:
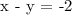
To be able to select which graph represents the equation, we will complete the coordinates of points at two conditions - when x = 0 and y = 0.
Once we get the set of coordinates, let's determine among the graphs which correctly reflects the two points.
Let's start,
First Point: At x = 0,
x - y = -2
0 - y = -2
-y/-1 = -2/-1
y = 2
(0,2)
Second Point: At y = 0,
x - y = -2
x - 0 = -2
x = -2
(-2,0)
We now got the coordinates of the two points that pass through the line graph of the equation. (0,2) and (-2,0)
Among the given graphs, naming A, B, C, D, E, F respectively from the upper left to the lower right, graph F reflects the correct coordinates of the two points we got.
Therefore, Graph F is the appropriate graph of the equation x - y = -2.