we have the expression
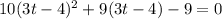
Let
x=3t-4
Change the variable
so
10x^2+9x-9=0
solve the quadratic equation using the formula
we have
a=10
b=9
c=-9
substitute
![x=\frac{-9\pm\sqrt[]{9^2-4(10)(-9)}}{2(10)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9jexnwy7xy6poeutnxuxb4b53e2gk8x9rq.png)
![\begin{gathered} x=\frac{-9\pm\sqrt[]{441}}{20} \\ \\ x=(-9\pm21)/(20) \\ x=(12)/(20)=(3)/(5) \\ \\ x=-(3)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8tqwvucs4sv4rayt2j1x6yh2itt4d55dop.png)
we have
x=3/5 and x=-3/2
Find the value of t
Remember that
x=3t-4
For x=3/5
3/5=3t-4
3t=3/5+4
3t=23/5
t=23/15
For t=-3/2
-3/2=3t-4
3t=-3/2+4
3t=5/2
t=5/6
therefore
the answer is
t=23/15 and t=5/6