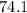Since the radius of the semicircle on the left part of the diagram is 3in, then its diameter must be equal to 6in. The diameter of that semicircle is the same as the height of the rectangle.
Find the area of the semicircle. Then, find the area of the rectangle and finally, find the area of the triangle. Add the areas of the three parts of the figure to find the total area of the award.
Semiricle:
The area of a semicircle is half the area of a circle. For a semicircle with radius r, the area is given by the following expression:
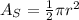
Substitute r=3in and use the given value for the constant:
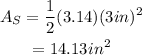
Rectangle
The area of a rectangle is equal to the product of its width and its height:
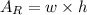
Substitute w=8in and h=6in:
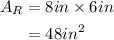
Triangle
The area of a triangle is equal to half the product of its base and its height:
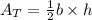
Substitute b=6in and h=4in:
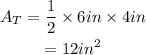
Award:
Add the three areas to find the total area of the award:
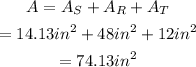
Therefore, the area of the award to the nearest tenth of a square inch, is: