Given two angles and one side of the triangle, you have to find the missing angle and the missing sides.
To do it, you can follow the steps.
Step 1: Find the missing angle.
Knowing that the sum of interior angles of a triangle is 180°, you can find A.
A + B + C = 180°
Knowing that B = 42° and C = 100°, you can substitute them in the equation and find A.
A + 42 + 100 = 180
A + 142 = 180
Adding - 142 to both sides:
A + 142 - 142 = 180 - 142
A + 0 = 38
A = 38°
Step 2: Find the missing sides.
Since all the angles and only one side are known, you can use the sen rule.
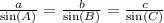
Substituting the values, you have:
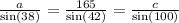
First, let's compare sides a and b:
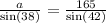
Multiplying both sides bi sin(38):

And solving the equation:
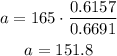
Now, let's find c by comparing b and c:

Multiplying both sides by sin(100) and solving the equation.

Done! You found the missing sides and angles.
As you can see, there is only one possible solution.
And the solution is:
a = 151.8; A = 38°
b = 165; B = 42°
c = 242.8; C = 100°