Given:
The third term of an arithmetic progression is,
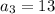
The thirteenth term of the arithmetic progression is,
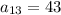
The objective is to find the 17th term of the sequence.
Step-by-step explanation:
The general formula for the nth term of an arithmetic sequence is,
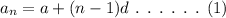
The expression for the third term can be written as,
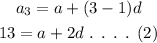
Similarly, the expression for the thirteenth term can be written as,
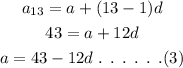
To find d:
Now, substitute equation (3) in equation (2).
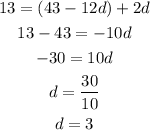
To find a :
Now, substitute the value of d in equation (3).
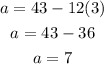
Thus, the value of a is 7 and the value of d is 3.
To find a17:
Now, the 17th term can be calculated from equation (1) as,

On further solving the above equation,
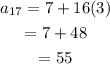
Hence, the value of a17 of the arithmetic progression is 55.value of a17 of thear