Question

Given the following information about the arithmetic sequence an, find a17.a3=13a13=43

Answer 1

Given:

The third term of an arithmetic progression is,

`a_3=13`

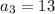
The thirteenth term of the arithmetic progression is,

`a_(13)=43`

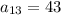
The objective is to find the 17th term of the sequence.

Step-by-step explanation:

The general formula for the nth term of an arithmetic sequence is,

`a_n=a+(n-1)d\text{ . . . . . . (1)}`

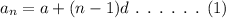
The expression for the third term can be written as,

`\begin{gathered} a_3=a+(3-1)d \\ 13=a+2d\text{ . . . . (2)} \end{gathered}`

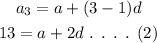
Similarly, the expression for the thirteenth term can be written as,

`\begin{gathered} a_(13)=a+(13-1)d \\ 43=a+12d \\ a=43-12d\text{ . . . . . .(3)} \end{gathered}`

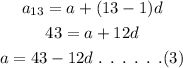
To find d:

Now, substitute equation (3) in equation (2).

`\begin{gathered} 13=(43-12d)+2d \\ 13-43=-10d \\ -30=10d \\ d=(30)/(10) \\ d=3 \end{gathered}`

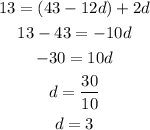
To find a :

Now, substitute the value of d in equation (3).

`\begin{gathered} a=43-12(3) \\ a=43-36 \\ a=7 \end{gathered}`

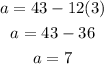
Thus, the value of a is 7 and the value of d is 3.

To find a17:

Now, the 17th term can be calculated from equation (1) as,

`a_(17)=7+(17-1)3`

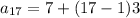
On further solving the above equation,

`\begin{gathered} a_(17)=7+16(3) \\ =7+48 \\ =55 \end{gathered}`

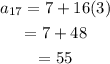
Hence, the value of a17 of the arithmetic progression is 55.value of a17 of thear