Question

Which of the following points lies on the line 2x+4y=10. Choices: (2,1) (-1,3) (-2,2) (2,2)

Answer 1

We need to substitute each point into the line in order to see if it belongs to the line.

If we substitute point (2,1) we have

`2(2)+4(1)=10`

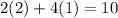
on the left hand side, we get

`4+4=8`

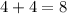
but 8 its not equal to 10, then this point doesnt belongs to the line.

Similarly, if we substitute poin (-1,3), we obtain

`\begin{gathered} 2(-1)+4(3)=10 \\ -2+12=10 \\ 10=10 \end{gathered}`

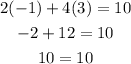
since both sides have the same value (10), then this point is on the line.

Now, if we substitute point (-2,2), we get

`\begin{gathered} 2(-2)+4(2)=10 \\ -4+8=10 \\ 4=10\text{ !!!} \end{gathered}`

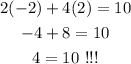
since both side are not equal, then this point doesnt belongs to the line.

Finally, if we substitute point (2,2), we obtain

`\begin{gathered} 2(2)+4(2)=10 \\ 4+8=10 \\ 12=10\text{ !!!} \end{gathered}`

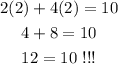
since both side are not equal, then this point doesnt belongs to the line.

Therefore, the points which belong to the line are: (2,1) and (-1,3)