In the function:
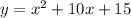
the coefficients are:
a = 1
b = 10
c = 15
Then, b/2 = 10/2 = 5. Computing the square of x and b/2, we get:
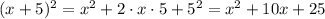
We can see that the first two terms coincide with the previous function, then we need to add and subtract 25 to that function to complete the square, as follows:
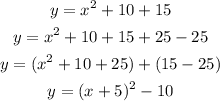
Solving the equation:
![\begin{gathered} (x+5)^2-10=0 \\ (x+5)^2=0+10 \\ (x+5)^2=10 \\ x+5=\sqrt[]{10} \\ This\text{ equation has 2 solutions:} \\ x_1=\sqrt[]{10}-5 \\ Or \\ x_2=-\sqrt[]{10}-5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6ecwu6jn6eqg2z4kntrc48so7caue6mu3k.png)