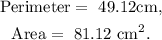To solve this question we will use the following diagram:
From the diagram, we get that the diameter of the semicircle is 8cm.
The perimeter of the figure is:
![P=14\operatorname{cm}+4\operatorname{cm}+6\operatorname{cm}+\pi\cdot8\operatorname{cm}\text{.}]()
Substituting π=3.14 and simplifying we get:
![\begin{gathered} P=14\operatorname{cm}+4\operatorname{cm}+6\operatorname{cm}+25.12\operatorname{cm}, \\ P=49.12\operatorname{cm}\text{.} \end{gathered}]()
Now, the area of the given figure is the area of the rectangle plus the area of the semicircle:
![A=14\operatorname{cm}*4\operatorname{cm}+\frac{\pi\cdot(4\operatorname{cm})^2}{2}\text{.}]()
Substituting π=3.14 and simplifying we get:
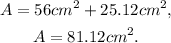
Answer: