Question

Write the coordinate proof of the following theorem: If a quadrilaterial is a kite, then diaonals are perpendicular.

Answer 1

we can do this by also finding the slope of the vertical diagonal which we will call m1 and the horizontal diagonal called m2

`\text{slope(m) = }(y_2-y_1)/(x_2-x_1)`

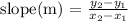
for m1, y2 =-c, y1 =c, x1=0 and x2 =0

`m_2=\frac{0-0}{b\text{ --a}}=\frac{0}{b\text{ +a}}=0`

The line joining cordinates (-a,0) and (b,0) has a slope of 0 which shows that it is a horizontal line and the the line with coordinates (0,c) and (0,-c) has an undefined slope which means the line is vertical

Hence with this proof the diagonals are perpandicular since for line perpendicular property, one line must be vertical and the other horizontal and they must cross each other at 0, hence the reason for 0 at y cordinates for the horizontal line and 0 at the x coordinates for the vertical line