Question

use casting out sevens to determine whether the following calculation could be correct.730, 963, 709x28, 100, 923, 561, 398 = 20, 450, 755, 312, 764, 971, 305, 182

Answer 1

We have to cast out sevens to find if the following operation is correct:

`730,963,709\cdot28,100,923,561,398=20,450,755,312,764,971,305,182​`

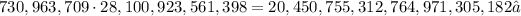
This method let us check if an aithmetic operation is correct by comparing the residues when dividing by 7.

For example, the correct operation:

`45+34=79`

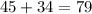
Will have residues: 45%7 = 3, 34%7 = 6 and 79%2. Then we can write the residues as:

`\begin{gathered} 3+6=2 \\ 9=2 \\ 9\%7=2 \\ 2=2\longrightarrow\text{Correct} \end{gathered}`

If we get the same residue after the divisions by 7, we can verify the operation.

We have veri large numbers.

We can estimate a big enough multiple of 7 and reduce the residues in steps.

For example, we can divide 730,963,709 by 700,000,000, which we know is a multiple of 7, and get a residue of 30,963,709.

For 28,100,923, we can divide by 28,000,000 and get a residue of 100,923.

For 20,450,755,312,764,971,305,182, we can divide by 14,000,000,000,000,000,000,000, and get a residue of 6,450,755,312,764,971,305,182.

We have to repeat the process until we can divide by 7 and get the minimal residues possible:

`\begin{gathered} 730,963,709\cdot28,100,923,561,398=20,450,755,312,764,971,305,182 \\ 30,963,709\cdot100,923,561,398=6,450,755,312,764,971,305,182 \\ 2,963,709\cdot2,923,561,398=150,755,312,764,971,305,182 \\ 163,709\cdot123,561,398=10,755,312,764,971,305,182 \\ 23,709\cdot53,561,398=3,755,312,764,971,305,182 \\ 2,709\cdot4,561,398=255,312,764,971,305,182 \\ 606\cdot361,398=45,312,764,971,305,182 \\ 46\cdot11,398=3,312,764,971,305,182 \\ 4\cdot4,398=512,764,971,305,182 \\ 4\cdot198=22,764,971,305,182 \\ 4\cdot58=1,764,971,305,182 \\ 4\cdot2=364,971,305,182 \\ 8=14,971,305,182 \\ 1=971,305,182 \\ 1=6,305,182 \\ 1=5,182 \\ 1=282 \\ 1=2 \end{gathered}`

As the residues are different, this indicates that the operation is not correct.

The actual result of the multiplication is:

`20,540,755,312,764,971,305,182`

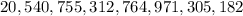
NOTE: the third and fourth digit are in inverse positions ("45" instead of the correct "54").

Answer: As the residues are different, we can conclude that the operation is incorrect.