Question

Find the exact value of cos (17π/6) by using the unit circle.

Answer 1

It is required to find the exact value of 17π/6 using the unit circle.

To do this, locate the angle on the unit circle to determine the point (x,y) it represents.

Recall that on the unit circle, the cosine is:

`\cos\theta=x`

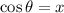
Since 17π/6 is greater than 2π, find its equivalent angle that is less than 2π by subtracting multiples of 2π until it is less than 2π:

`(17\pi)/(6)-2\pi=(5\pi)/(6)`

Locate this point on the unit circle:

From the unit circle, it can be seen that:

`x=-(√(3))/(2)\text{ and }y=(1)/(2)`

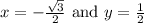
Hence, the required value is:

`\cos(17\pi)/(6)=-(√(3))/(2)`

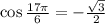
The answer is the first option.