Question

2 STEP PROBLEM:STEP 1 of 2: 9x^2 = 64 Using the standard form ax^2 + bx + c = 0 of the given quadratic equation, factor the left hand side of the equation into two linear factors. STEP 2 of 2: 9x^2 = 64Solve the quadratic equation by factoring. Write your answer in reduced fraction form, if necessary.

Answer 1

Step 1:

The equation given can be written as:

`9x^2-64=0`

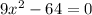
Using the general formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

we have that:

`\begin{gathered} x=\frac{-0\pm\sqrt[]{0^2-4(9)(-64)}}{2(9)} \\ x=\frac{\pm\sqrt[]{2304}}{18} \\ x=(\pm48)/(18) \\ x=(\pm8)/(3) \end{gathered}`

This means that we can factor the equation as:

`\begin{gathered} (x-(8)/(3))(x+(8)/(3))=0 \\ (3x-8)(3x+8)=0 \end{gathered}`

Therefore the factorization is:

`(3x-8)(3x+8)=0`

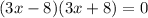
Another way to do this is by noticing that the equation:

`9x^2-64=0`

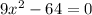
is a difference of squares, using the general formula for difference of squares:

`x^2-y^2=(x-y)(x+y)`

Using this we get the same result as before:

`(3x-8)(3x+8)=0`

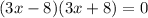
Step 2:

From the factorization and using the fact that the multiplication between two numbers can only be zero if one of them is zero we have that:

`\begin{gathered} (3x-8)(3x+8)=0 \\ \text{if and only if} \\ 3x-8=0 \\ or \\ 3x+8=0 \end{gathered}`

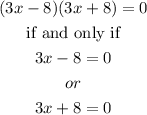
Solving each linear equation we have that:

`\begin{gathered} 3x-8=0 \\ 3x=8 \\ x=(8)/(3) \end{gathered}`

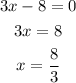
or

`\begin{gathered} 3x+8=0 \\ 3x=-8 \\ x=-(8)/(3) \end{gathered}`

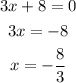
Therefore the solutions of the equation are x=8/3 and x=-8/3