Given that collection of nickels and quarters equals 61, thus;
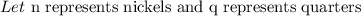

Also, 1 dollar is equal to 20 nickels;
Hence 1 nickel is 1/20 dollars = $0.05;
Similarly, 1 quarter is $0.25, thus;

Solving the two equations simultaneously;

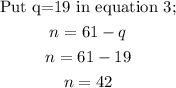
Hence, Azlyn has 42 nickels and 19 quarters