Question

Which pair of liens are perpendicular?y = -8 and y = 2Ox – y = 7 and y = x + 3x = 4 and y = -1O y= -4x + 1 and 8x + 2y = -10

Answer 1

Two lines are parallel if their slopes are the same

Two lines are perpendicular if the products of their slopes = -1

To get the slopes, we can compare the equation of the line to the general equation of a line in slope-intercept form (y=mx+c)

Looking at the options given

Option 1

Not correct

Option 2

`\begin{gathered} x-y=7 \\ y=x-7 \end{gathered}`

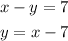
and

`y=x+3`

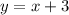
The slope of the two lines = 1

hence, Not correct

Option 3

This option is correct because the plot of the two lines on a graph are perpendicular

The plot is shown below

Option 4

`\begin{gathered} y=-4x+1 \\ \text{slope}=\text{ -4} \end{gathered}`

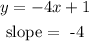
for

`\begin{gathered} 8x+2y=-10 \\ \text{make y the subject of the formula} \\ 2y=-8x+10 \\ \text{Divide both sides by 2} \\ y=-4x+5 \end{gathered}`

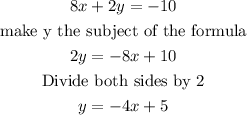
Hence, the slope is the same.

so the option is not correct