Question

I need help on question 3b. i and iiI have already done a

Answer 1

Given:

• Number of people who like only bananas = 12

,

• Number of people who like only pies = 11

,

• Number of people who like both = 7

,

• Number of people who like neither = 3

Let's solve for the following:

• b(i). Given that a person is chosen at random, let's find the probability that the person likes banana.

To find the probability, apply the formula:

`P(banana)=\frac{number\text{ of people who like banana}}{total\text{ number of people surveyed}}`

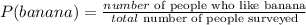
Where:

Total number of people surveyed = 12 + 11 + 7 + 3 = 33

Number of people who like banana = 12 + 7= 19

Thus, we have:

`P(bananas)=(19)/(33)`

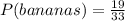
Therefore, the probability that a person chosen randomly likes bananas is 19/33.

• b(ii). ,Given that a person is chosen at random, let's find the probability that the person doesn't like pie.

To find the probability, apply the formula:

`\begin{gathered} P(doesn^(\prime)t\text{ like pie\rparen = 1-}\frac{}{}P(people\text{ who like pie\rparen} \\ \\ P(doesn^(\prime)t\text{ like pie\rparen = 1-}\frac{number\text{ of people who like pie}}{total\text{ number of people}} \end{gathered}`

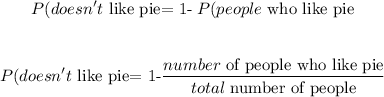
Where:

Number of people who like pie = 11 + 7 = 18

Total number of people = 33

Thus, we have:

`\begin{gathered} P(doesn^(\prime)t\text{ like pie\rparen = 1-}(18)/(33) \\ \\ =(33-18)/(33) \\ \\ =(15)/(33) \end{gathered}`

The probability that a person chosen at random doesn't like pie is 15/33.

ANSWER:

• b(i). 19/33

• b(ii). 15/33