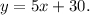To answer this question we will use the following slope-point formula for the equation of a line:
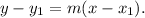
Recall that two lines are parallel if they have the same slope.
Now, notice that the given equation is y=5x, therefore, the slope of the given equation is 5.
Using the slope-point formula, we get that the equation of the parallel line to y=5x that passes through (-5,5) is:
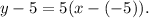
Simplifying the above equation we get:
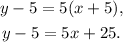
Adding 5 to the above equation we get:
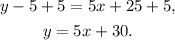
Answer: