a = 15, b = 29 and c = 23
A= 31º B= 97º C= 52º
1) To solve a triangle is to find out its angles and measures. Since we have angle A= 31º, C =52º, and b= 29 we can solve this by using the Sum of Interior angles and the Law of sines:
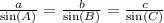
2) The sum of the interior angles of a Triangle is 180º So, we can find angle B this way
∠A +∠B+∠C= 180º
31º +∠B +52º = 180º
∠B + 83º = 180º Subtract 83 from both sides
∠B =97º
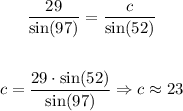
2.2) Now we can find the leg "a "
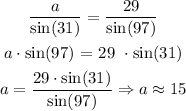
3) Hence, the answer is
a = 15, b = 29 and c = 23
A= 31º B= 97º C= 52º