Given: The sine graph shown in the image
To Determine: The amplitude, the period and the sine function
Solution
The general sine function is as shown below
From the given graph,
The amplitude is
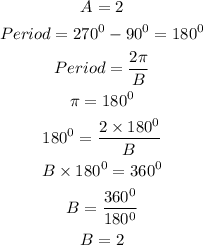
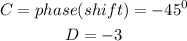
So, the function of the graph would be
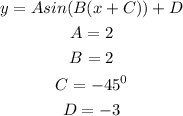
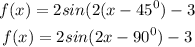
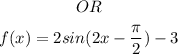
Hence, the sine function of the given graph is
y = 2sin(2x - 90⁰) - 3
OR
y = 2sin(2x - π/2) - 3