Question

Which system of linear inequalities has the point (3 -2) in its solution set

Answer 1

The first system is:

`\begin{gathered} y<-3 \\ y<(2)/(3)x-4 \end{gathered}`

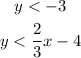
Its graph is the following:

In this graph, we can see that the purple zone is the solution of the system and point (3,-2) is not there.

The second system is:

`\begin{gathered} y>-3 \\ y\ge(2)/(3)x-4 \end{gathered}`

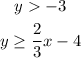
Its graphs is give by

In this graph, we can note that the purple zone is the solution and point (3,-2) is in the boundary. Since the boundary is part of the solution, then the given point is contained in the solution.

The third system is:

`\begin{gathered} y>-2 \\ y\le(2)/(3)x-4 \end{gathered}`

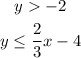
Its graph is the following:

From this graph, we can see that point (3,-2) is in the corner of the solution, which is the red zone. Since the corner does not belongs to the solution, then the given point is not a solution because y must be greater than -2, strictly.

In summary, the answer is option 2