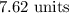Answer:
The length of the line segment is;
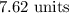
Step-by-step explanation:
Given the line segment in the attached image.
Drawing a right angled triangle to get the length of the line segment;
We can then use pythagoras theorem to calculate length of the line segment;
![c=\sqrt[]{a^2+b^2}](https://img.qammunity.org/2023/formulas/mathematics/college/6uwqakmkjq6nua21bpopztkrf20jt2flji.png)
From the attached image;
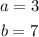
substituting the given values;
![\begin{gathered} c=\sqrt[]{3^2+7^2} \\ c=\sqrt[]{9+49} \\ c=\sqrt[]{58} \\ c=7.62\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h4nqgensbxe6wh7uh5fvfnb981v28gw0oi.png)
Therefore, the length of the line segment is;