Question

Hi there. I am completely lost here. Can you help me out?

Answer 1

We have a diagram for chords in a circle.

Given that OE = 25, AB = 40 and CD = 30, we have to find the length of the other segments in the list.

We start with MB, which will be half the length of AB because OE is a perpendicular bisector.

Then:

`MB=(AB)/(2)=(40)/(2)=20`

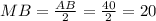
For OB we can consider that it is a radius, as O is the center and B is a point on the circumference. As the radius is constant in a circle and we know that OE = 25, then OB should also be OB = 25.

Given OB = 25 ad MB = 20, we can use the Pythagorean theorem to find OM as:

`\begin{gathered} OM^2+MB^2=OB^2 \\ OM^2=OB^2-MB^2 \\ OM^2=25^2-20^2 \\ OM^2=625-400 \\ OM^2=225 \\ OM=√(225) \\ OM=15 \end{gathered}`

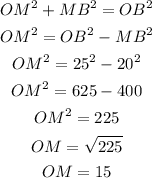
Now we calculate ND. As OE is a perpendicular bisector of CD, we have:

`ND=(CD)/(2)=(30)/(2)=15`

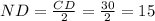
The segment OD is a radius so it has a length like OE. Then, OD = 25.

For the segment ON we can use the Pythagorean theorem again:

`\begin{gathered} ND^2+ON^2=OD^2 \\ ON^2=OD^2-ND^2 \\ ON^2=25^2-15^2 \\ ON^2=625-225 \\ ON^2=400 \\ ON=√(400) \\ ON=20 \end{gathered}`

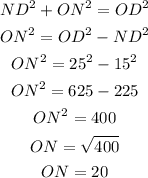
The last segment is MN which length can be expressed as the difference of the lengths of ON and OM:

`MN=ON-OM=20-15=5`

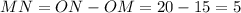
Answer:

MB = 20

OB = 25

OM = 15

ND = 15

OD = 25

ON = 20

MN = 5