Hello there. To solve this question, we'll have to remember some properties about factorization.
Given the following polynomials, we have to decide whether they are factorable (presumably over the real numbers). If they are not, we have to change the constant term so that it turns into a perfect square trinomial.
a) p² + 12p + 33
As this is a second degree polynomial, we can decide if it is factorable by calculating its discriminant:
For a second degree polynomial with real coefficients ax² + bx + c, it is factorable if and only if:
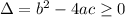
Plugging in a = 1, b = 12 and c = 33, we get:
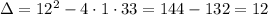
Therefore this polynomial can be factored.
Its factored form will be something as follows:
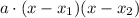
Where a is the leading coefficient of the polynomial, x1 and x2 are its roots.
We calculate the roots by using the quadratic formula, for a not equal to 0:
![x_(1,2)=\frac{-b\pm\sqrt[]{\Delta}_{}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/avjvwynvtrod70lu357lw2ykly0bnrnyy7.png)
Plugging the values, we get:
![x_(1,2)=\frac{-12\pm\sqrt[]{12}}{2\cdot1}=\frac{-12\pm\sqrt[]{4\cdot3}_{}}{2}=\frac{-12\pm2\sqrt[]{3}_{}}{2}=-6\pm\sqrt[]{3}_{}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zc3vju12gh0gm35sy6kmi9qqgz6mnhpl48.png)
We break the solutions, such that
![\begin{gathered} x_1=-6-\sqrt[]{3} \\ x_2=-6+\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qvy1w2gqhs5eqsa8taeowrzpef2a3red3c.png)
And the factored form is:
![\begin{gathered} 1\cdot(p-(-6-\sqrt[]{3}))(p-(-6+\sqrt[]{3})) \\ (p+6+\sqrt[]{3})(p+6-\sqrt[]{3}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7wkbgxymiveuzqlw2tybjx4r4j4xg0e1a9.png)
Rewriting it as a perfect square trinomial, that is, something of the form:

We have to take the coefficient b and divide by two. After this, we square the result and plug as the new constant term:
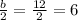
Squaring the number
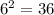
This is the new constant term, such that the perfect square trinomial is then:
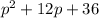
b) x² - 16x + 61
Again, we check if it can be factored by plugging the coefficients in the formula for the discriminant:

And this is a factorable polynomial.
Its factored form will be:
![(x-8+\sqrt[]{3})(x-8-\sqrt[]{3})](https://img.qammunity.org/2023/formulas/mathematics/high-school/9099d0x71z1ecilzdzkplvrmfu209bzmzv.png)
But to answer the question, we have to rewrite it as a perfect square polynomial.
In order to do so, we repeat the process, this time using b = -16:
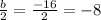
Square the number
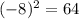
This is the new constant term, such that:
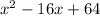
Is the perfect square trinomial we were looking for.