Question

Complete the square to solve the equation below.x2 - 10x - 2 = 17A. X= 5+ 29x= 5 - 29B. x = 5 + 144 ; x = 5 - 444C. x = 5+ V55, x = 5- 55D. X = 6 + 30; x = 6 - 30

Answer 1

`x^2-10x-2=17`

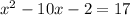
The coefficient next to the x-variable is b = -10. To complete the square, first, we need to compute the next term:

`(\frac{b^{}}{2})^2=(\frac{-10^{}}{2})^2=(-5)^2=25`

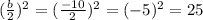
Adding and subtracting 25 to the first equation:

`\begin{gathered} x^2-10x-2+25-25=17 \\ (x^2-10x+25)-2-25=17 \\ (x-5)^2-27=17 \\ (x-5)^2-27+27=17+27 \\ (x-5)^2=44 \\ \sqrt[]{\mleft(x-5\mright)^2}=\sqrt[]{44} \\ x-5=\sqrt[]{44} \end{gathered}`

The square root of 44 has two different solutions, one positive and one negative. This lead to two different solutions for x:

`\begin{gathered} x_1-5=\sqrt[]{44} \\ x_1-5+5=\sqrt[]{44}+5 \\ x_1=5+\sqrt[]{44} \\ And \\ x_2-5=-\sqrt[]{44} \\ x_2-5+5=-\sqrt[]{44}+5 \\ x_2=5-\sqrt[]{44} \end{gathered}`