Question

Find the value of x. Round tothe nearest tenth.27°х34°11x = [?]Law of Sines: sin Asin B==bIIsin Cсa

Answer 1

We have the triangle and we must find the value of x.

To find the value of x we need to use the Law of Sines

- a is the opposite side to the angle A

- b is the opposite side to the angle B

- c is the opposite side to the angle C

So, seeing the triangle we can take values as

angle A = 27°, so a = 11

angle B = 34°, so b = x

Replacing in the law of Sines

`(\sin27\degree)/(11)=(\sin34\degree)/(x)`

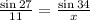
Finally, we must solve the equation for x

`\begin{gathered} (\sin27\degree)/(11)=(\sin34\degree)/(x) \\ \sin 27\degree\cdot x=\sin 34\degree\cdot11 \\ x=(\sin 34\degree\cdot11)/(\sin 27\degree) \\ x=13.5 \end{gathered}`

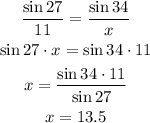
ANSWER:

x = 13.5