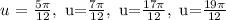Question

Algebraically, how can I find the exact solutions of the equation sqrt3 +2cos(2u)=0 in the interval [0,2pi)

Answer 1

Consider the following trigonometric equation:

`\sqrt[]{3}+2\cos (2u)=0`

to solve this equation, subtract the root of 3 from both sides of the equation, to obtain:

`2\cos (2u)=-\sqrt[]{3}`

now, solving for cos(2u), we get:

`\cos (2u)=-\frac{\sqrt[]{3}}{2}`

now, by the trigonometric circle, the general solutions for the above equation are:

`2u\text{ = }(5\pi)/(6)+2\pi n\text{ , 2u = }(7\pi)/(6)+2\pi n\text{ }`

now, if we solve the above equations for u, we get the following general solutions:

`u\text{ = }(5\pi)/(12)+\pi n\text{ , u = }(7\pi)/(12)+\pi n\text{ }`

so, for the interval [0,2pi), the solution would be:

`u\text{ = }(5\pi)/(12),\text{ u=}(7\pi)/(12),\text{ u=}(17\pi)/(12),\text{ u=}(19\pi)/(12)`