Question

A see saw 5 m long with a mass of 18 kg has a 31 kg child seated 0.3 m from the left edge. the pivot is located 2 m from the left edge of the see saw. if the child sits 3.9 m from the left edge, what must the mass of the second child be to balance the system?

Answer 1

First, draw a diagram to visualize the situation:

As we can see in the diagram, the distance from the center of mass of the bar to the pivot is 0.5m, and the distance from the children to the pivot are 1.7m from the 31kg child, and 1.9m for the unknown mass child.

From the second equilibrium condition, we know that the net torque on the system must be equal to 0 for the system to be balanced.

It can then be deduced that:

`\left(1.7m\right)(31kg)=\left(0.5m\right)(18kg)+(1.9m)* m`

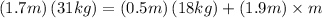
Where m is the unknown mass of the second child.

Solve for m:

`\begin{gathered} \left(1.7m\right)(31kg)=\left(0.5m\right)(18kg)+(1.9m)* m \\ \\ \Rightarrow m=((1.7m)(31kg)-(0.5m)(18kg))/(1.9m)=23kg \end{gathered}`

Therefore, the mass of the second child must be 23kg.