Question

What is the value of x based on the image

Answer 1

This question has two steps, one is trigonometry, which should get us an equation to work with.

The second is algebra where we will have to use the equation we got to find x.

Assuming R is the center of the circle, we can see that the central angle ∠SRU is not equal to a value, but an expression:

`\angle SRU=2x-32\degree`

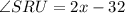
And the inscribed angle ∠STU has the value 70°:

`\angle STU=70\degree`

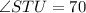
The value of an inscribed angle is the same as half the its central angle. This means that the value of ∠STU should be equal to half the value of ∠SRU:

`\angle STU=(\angle SRU)/(2)`

Now, we can input the values we have for these angles:

`70\degree=(2x-32\degree)/(2)`

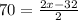
Now, the trigonometric part ended, and we just have to solve the equation for x:

`\begin{gathered} 70\degree=(2x-32\degree)/(2) \\ (2x-32\degree)/(2)=70\degree \\ 2x-32\degree=2\cdot70\degree \\ 2x-32\degree=140\degree \\ 2x=140\degree+32\degree \\ 2x=172\degree \\ x=(172\degree)/(2) \\ x=86\degree \end{gathered}`

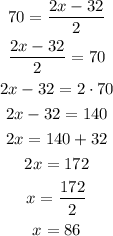
So, the value of x is 86°.