The simple interest formula is given by
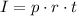
where I is the interest, p is the principal, r is the interest rate and t the time in years.
In our case,
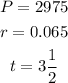
However, in order to use the above formula, we must convert the time into a simple fraction form, that is
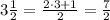
Then, by subsituting our values into the simple interest formula, we get
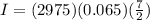
which gives
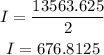
Then,by rounding to the nearest cent, the interest is $676.81